OpenGL 101: Matrices - projection, view, model
Posted on May 22, 2013 by Paul
The code for this post is on GitHub: https://github.com/sol-prog/OpenGL-101.
This is the fourth article from my OpenGL 101 series, if you need to refresh your memory you can find a list with my previous articles at the end of this post or, you can click on the OpenGL category from the right sidebar.
Until now we’ve used the default OpenGL view for drawing our geometries and textures. While it is possible to draw any 2D geometry we can think of using the default [-1, +1] x [-1, +1] space that OpenGL sets for us, it will quickly became cumbersome and inefficient. Consider the problem of drawing four equilateral triangles, with different positions and orientations, like in the following figure:
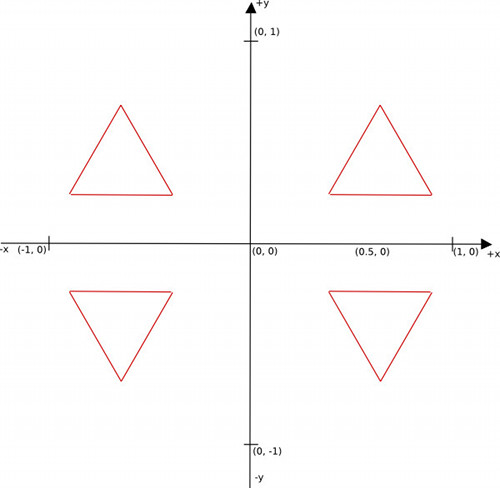
A possible solution is to store all four triangle coordinates in an array, like in our previous article. What if, instead of four we’d have twenty triangles spread on our screen ? In the later case we’ll need to store 60 vertices in our array. Now, imagine that you have a complex object made from a certain number of triangles, with his surface painted with one or more textures. Say that we want to replicate this object a few times on our screen at various positions and orientations. Clearly, we need a better way to do this than to store the object in all possible positions and orientations.
Fortunately for us, this is a solved problem in computer graphics, but it involves a bit of matrix algebra. Instead of storing an object N times, we will store the object a single time and use geometrical transformations like translations, rotations and scaling to place the object where we need it.
In the next figure we exemplify the concept of geometrical transformations using a square:
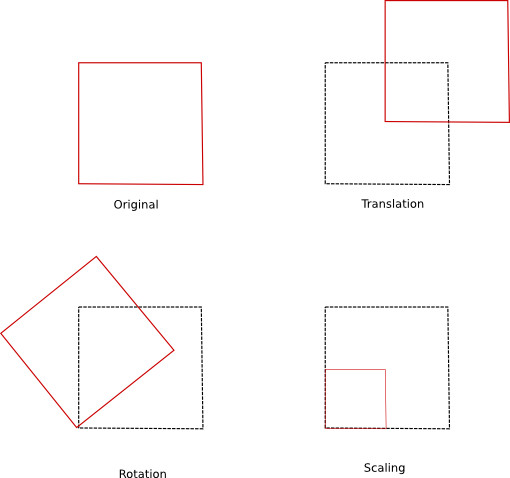
The above figure presents individual transformations applied to a square. These simple transformations can be combined, if we need to achieve more complex transformations:
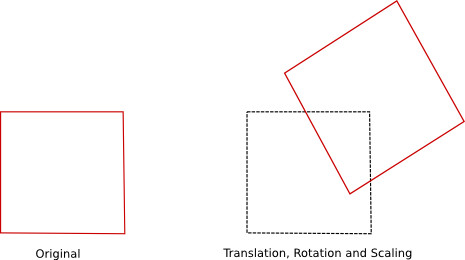
So, how do we translate an object in our OpenGL code ? We start, as usual, by transferring the object coordinates to an OpenGL buffer and we multiply the object coordinates with a translation matrix in the vertex shader program.
If you don’t know what a matrix is or what matrix multiplication means, I’ve included a quick introduction in the next few paragraphs. You can use this as a quick refresher even if you’ve worked with matrix algebra concepts in the past. Please note that this is not an exhaustive presentation of matrix algebra, we barely scratch the tip of the iceberg here. I’ve included at the end of this article a link to two good introductory books in matrix algebra for game design and computer graphics, if you want to learn more about this subject.
Matrix algebra refresher
Mathematically, a matrix is a rectangular grid of numbers. We can identify a number, or an element, in a matrix by his corresponding row number and column.
\[\left[ {\begin{array}{*{20}{c}} a&b&c&d \\ e&f&g&h \\ i&j&k&l \end{array}} \right]\]For example h in the above matrix is on the second row and fourth column.
We indicate that a matrix M has m rows and n columns using the notation:
\[{M_{m,n}}\]A matrix that has the number of rows equal to the number of columns is named square.
We say that a square matrix is diagonal if all the elements are zero except for the ones from the main diagonal:
\[\left[ {\begin{array}{*{20}{c}} a&0&0 \\ 0&b&0 \\ 0&0&c \end{array}} \right]\]The identity matrix is a diagonal matrix with every diagonal element equal to 1, the identity matrix is usually denoted as I:
\[I = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{array}} \right]\]A matrix with n rows and 1 column is named a column vector:
\[\left[ {\begin{array}{*{20}{c}} 1 \\ 2 \\ 3 \end{array}} \right]\]A matrix with 1 row and n columns is named a row vector.
\[\left[ {\begin{array}{*{20}{c}} 1&2&3&4 \end{array}} \right]\]Matrix transposition - if we have a matrix M with n rows and m columns, the transpose of \(M\), denoted \({M^T}\) is a matrix with m rows and n columns, with the first column of \({M^T}\) equal to the first row of \(M\) and so on. Example:
\[M = \left[ {\begin{array}{*{20}{c}} a&b&c&d \\ e&f&g&h \\ i&j&k&l \end{array}} \right]\] \[{M^T} = \left[ {\begin{array}{*{20}{c}} a&e&i \\ b&f&j \\ c&g&k \\ d&h&l \end{array}} \right]\]As a side note, if we transpose a column vector we obtain a row vector and vice-versa.
Matrix addition - two matrices of the same dimensions can be summed, we add them element by element. Example:
\[\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 2&3 \\ 4&5 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1 + 2}&{0 + 3} \\ {0 + 4}&{1 + 5} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 3&3 \\ 4&6 \end{array}} \right]\]For matrix subtraction we proceed in the same way, we subtract them element by element. Example:
\[\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} 2&3 \\ 4&5 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1 - 2}&{0 - 3} \\ {0 - 4}&{1 - 5} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 1}&{ - 3} \\ { - 4}&{ - 4} \end{array}} \right]\]Matrix multiplication with a scalar (or matrix multiplication with a number) is the operation of multiplying every element of the matrix with a scalar. Example:
\[2 \cdot \left[ {\begin{array}{*{20}{c}} 1&2&3 \\ 4&5&6 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {2 \cdot 1}&{2 \cdot 2}&{2 \cdot 3} \\ {2 \cdot 4}&{2 \cdot 5}&{2 \cdot 6} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 2&4&6 \\ 8&{10}&{12} \end{array}} \right]\]Matrix multiplication - if we have two matrices \({A_{m,n}}\) and \({B_{n,p}}\), the result of the multiplication is a new matrix \({C_{m,p}}\). The first element of C can be obtained by taking the first row of A and first column of B, multiplying them element by element and summing the result. Second element of C, from the first line, can be obtained by multiplying the first line of A with the second column of B and summing the result …
Example:
\[\left[ {\begin{array}{*{20}{c}} 1&2&3 \\ 2&4&0 \\ 5&{ - 1}&2 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1&2 \\ 4&5 \\ 1&0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1 \cdot 1 + 2 \cdot 4 + 3 \cdot 1}&{1 \cdot 2 + 2 \cdot 5 + 3 \cdot 0} \\ {2 \cdot 1 + 4 \cdot 4 + 0 \cdot 1}&{2 \cdot 2 + 4 \cdot 5 + 0 \cdot 0} \\ {5 \cdot 1 - 1 \cdot 4 + 2 \cdot 1}&{5 \cdot 2 + ( - 1) \cdot 5 + 2 \cdot 0} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {12}&{12} \\ {18}&{24} \\ 3&5 \end{array}} \right]\]In order to be able to multiply two matrices, A and B, the number of columns of A must be equal to the number of rows of B. The resulting matrix will have as dimensions - the number of rows of A and the number of columns of B. This is also suggested by the notation:
\[{A_{m,n}} \cdot {B_{n,p}} = {C_{m,p}}\]Important properties of matrix multiplication:
- Matrix multiplication is not commutative, or, more explicitly, in general:
- Matrix multiplication is associative:
- The transpose of the product of two matrices is the product, in inverse order, of each matrix transposed:
An interesting property of the identity matrix is that:
\[A \cdot I = I \cdot A = A\]Since a vector is basically a matrix (with dimensions 1xn or nx1), multiplying a vector with a matrix, or a matrix with a vector, obeys the same rules as the matrix multiplication. Examples:
\[\left[ {\begin{array}{*{20}{c}} 1&2&3 \\ 2&4&0 \\ 5&{ - 1}&2 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1 \\ 4 \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1 \cdot 1 + 2 \cdot 4 + 3 \cdot 1} \\ {2 \cdot 1 + 4 \cdot 4 + 0 \cdot 1} \\ {5 \cdot 1 + ( - 1) \cdot 4 + 2 \cdot 1} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {12} \\ {18} \\ 3 \end{array}} \right]\] \[\left[ {\begin{array}{*{20}{c}} 1&4&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1&2&3 \\ 2&4&0 \\ 5&{ - 1}&2 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {14}&{17}&5 \end{array}} \right]\]The model matrix
As suggested earlier, we can apply various geometrical transformations on an object using matrices. If we need to rotate an object, we multiply his coordinates with a rotation matrix, same goes for translation and scaling. The order in which we apply these transformations to an object is essential. We will achieve different effects if we translate and apply a rotation to an object than if we start by rotating the object and translating the result.
From a mathematical point of view applying two, or more, transformations to an object can be done by multiplying the object coordinates with elementary matrix transformations one by one. Alternatively, we can use a single matrix, that contains all the above transformations, to multiply the object coordinates:
\[R \cdot T \cdot v = M \cdot v\]where:
\[M = R \cdot T\]and v is a column vector that contains a vertex from our object. In order to properly transform an object, the transformation must be applied to every vertex of the object.
In the above equations we’ve replaced the product of two transform matrices, R (rotation) and T (translation), with a single transform matrix, M, using the associativity property of the matrix multiplication.
The matrix M, that contains every translations, rotations or scaling, applied to an object is named the model matrix in OpenGL. Basically, instead of sending down the OpenGL pipeline two, or more, geometrical transformation matrices we’ll send a single matrix for efficiency. Remember that the vertex shader program is executed for every vertex ? It is more efficient to multiply the coordinates of every vertex with a single model matrix than to do it with two or more matrices.
Without further ado, these are the geometrical transformation matrices for a 3D vertex:
- Translation:
The above array will translate a vector, v, with \({T_x}\) in the x direction, \({T_y}\) in the y direction, etc …
- Rotation:
For rotation we have three matrices, corresponding to the Ox, Oy and Oz axes. For example, \({R_z}\) will rotate a vector v with \(\alpha\) degrees around the Oz axis counterclockwise.
- Scaling:
The above array will scale a vector, v, with \({S_x}\) in the x direction, \({S_y}\) in the y direction, etc …
Please note that the above matrices are 4x4 matrices and not 3x3 matrices! This is because the translation matrix can’t be written as a 3x3 matrix and we use a mathematical trick to express the above transformations as matrix multiplications. An interesting consequence of working with 4x4 matrices instead of 3x3, is that we can’t multiply a 3D vertex, expressed as a 3x1 column vector, with the above matrices. Instead we’ll use the so called homogeneous coordinates, where a 3D vertex can be expressed as a 4x1 column vector. From our point of view, this simply means that we’ll write a 3D vertex as:
\[v = \left[ {\begin{array}{*{20}{c}} x \\ y \\ z \\ w \end{array}} \right]\]where w = 1.
If we want to transform a vertex from the homogeneous space to the 3D Cartesian space we could use:
\[v = \left[ {\begin{array}{*{20}{c}} x/w \\ y/w \\ z/w \end{array}} \right]\]Let’s try, for e. g., to rotate a 2D vertex, x = 0.5 and y = 0.5, with \(\alpha = {90^\circ }\) around Oz:
\[\left[ {\begin{array}{*{20}{c}} {\cos \left( {90 \cdot \frac{\pi }{180}} \right)}&{ - \sin \left( {90 \cdot \frac{\pi }{180}} \right)}&0&0 \\ {\sin \left( {90 \cdot \frac{\pi }{180}} \right)}&{\cos \left( {90 \cdot \frac{\pi }{180}} \right)}&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {0.5} \\ {0.5} \\ 0 \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0&0 \\ 1&0&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {0.5} \\ {0.5} \\ 0 \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 0.5} \\ {0.5} \\ 0 \\ 1 \end{array}} \right]\]The result of the above multiplication is the position of the rotated vertex, x = -0.5, y = 0.5. As a side note, I’ve transformed the angle from degrees to radians in the above matrix. As you probably know, you need to use radians for angles in order to use the trigonometrical functions in C or C++.
Say, that your intention was to translate the vertex obtained after applying the above rotation with 0.1 on x, -0.2 on y and 0.5 on z:
\[\left[ {\begin{array}{*{20}{c}} 1&0&0&{0.1} \\ 0&1&0&{ - 0.2} \\ 0&0&1&{0.5} \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} { - 0.5} \\ {0.5} \\ 0 \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 0.4} \\ {0.3} \\ {0.5} \\ 1 \end{array}} \right]\]Let’s write the above two transformations using the model matrix:
\[M = \left[ {\begin{array}{*{20}{c}} 1&0&0&{0.1} \\ 0&1&0&{ - 0.2} \\ 0&0&1&{0.5} \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\cos \left( {90 \cdot \frac{\pi }{180}} \right)}&{ - \sin \left( {90 \cdot \frac{\pi }{180}} \right)}&0&0 \\ {\sin \left( {90 \cdot \frac{\pi }{180}} \right)}&{\cos \left( {90 \cdot \frac{\pi }{180}} \right)}&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] = \\ = \left[ {\begin{array}{*{20}{c}} 1&0&0&{0.1} \\ 0&1&0&{ - 0.2} \\ 0&0&1&{0.5} \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0&0 \\ 1&0&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0&{0.1} \\ 1&0&0&{ - 0.2} \\ 0&0&1&{0.5} \\ 0&0&0&1 \end{array}} \right]\]And now, we can rotate and translate the original vertex with:
\[\left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0&{0.1} \\ 1&0&0&{ - 0.2} \\ 0&0&1&{0.5} \\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {0.5} \\ {0.5} \\ 0 \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 0.4} \\ {0.3} \\ {0.5} \\ 1 \end{array}} \right]\]The view matrix
By default, in OpenGL, the viewer is positioned on the z axis, it is like using a camera to take a shot. Imagine that your camera points to the origin of the Cartesian system. The up direction is parallel to the Oy axis and in the positive sense of Oy.
The view matrix in OpenGL controls the way we look at a scene. In this article we are going to use a view matrix that simulates a moving camera, usually named lookAt.
It is beyond the purpose of the present article to derive and present the way we create the view matrix, suffice to say that it is a 4x4 matrix, like the model matrix, and it is uniquely determined by 3 parameters:
-
The eye, or the position of the viewer;
-
The center, or the point where we the camera aims;
-
The up, which defines the direction of the up for the viewer.
The defaults in OpenGL are: the eye at (0, 0, -1); the center at (0, 0, 0) and the up is given by the positive direction of the Oy axis (0, 1, 0).
Suppose that we have a generic C++ function that given the eye, the center and the up will return a 4x4 view matrix for us.
The view matrix, V, multiplies the model matrix and, basically aligns the world (the objects from a scene) to the camera. For a generic vertex, v, this is the way we apply the view and model transformations:
\[v' = V \cdot M \cdot v\]The projection matrix
By default, in OpenGL, an object will appear to have the same size no matter where the camera is positioned. This is against our day to day experience, where an object closer to us (to the camera) looks larger than an object that is at a greater distance. Picture the way a ball approaches you, the ball will appear bigger and bigger as it is closer to your eyes.
Another problem with the defaults from OpenGL is that in order to actually see (draw) something on the screen, the objects that we intend to draw must be inside the cube [-1, +1] x [-1, +1] x [-1, +1]. Any part of our scene that is outside the unit cube will be clipped.
We can virtually enlarge or shrink the clipping volume through the use of a projection matrix, when our clipping volume has the shape of a parallelepiped, or a box, we say that we use an orthographic projection. The orthographic projection will not modify the size of the objects no matter where the camera is positioned. This is a desirable characteristic for CAD programs or for 2D games.
The orthographic projection matrix:
\[P = \left[ {\begin{array}{*{20}{c}} {\frac{2}{right - left}}&0&0&{ - \frac{right + left}{right - left}} \\ 0&{\frac{2}{top - bottom}}&0&{ - \frac{top + bottom}{top - bottom}} \\ 0&0&{ - \frac{2}{far - near}}&{ - \frac{far + near}{far - near}} \\ 0&0&0&1 \end{array}} \right]\]Where right, left, far, near, top, bottom represents the positions of the clipping planes. Can you guess what is the orthographic projection matrix used by default in OpenGL. Hint, use the cube [-1, +1] x [-1, +1] x [-1, +1] to define your right, left …
Another projection matrix, that can enhance the feeling of real world is the perspective projection matrix, in this case the volume is a frustum and not a parallelepiped.
The perspective projection matrix is:
\[P = \left[ {\begin{array}{*{20}{c}} {\frac{2 \cdot near}{right - left}}&0&{\frac{right + left}{right - left}}&0 \\ 0&{\frac{2 \cdot near}{top - bottom}}&{\frac{top + bottom}{top - bottom}}&0 \\ 0&0&{ - \frac{far + near}{far - near}}&{ - \frac{2 \cdot far \cdot near}{far - near}} \\ 0&0&{ - 1}&0 \end{array}} \right]\]The perspective projection matrix is usually specified through four parameters:
-
viewing angle or field of view (usually abbreviated as FOV);
-
aspect
-
near and far
Where near and far represent the positions of the near and the far clipping planes.
\[\begin{gathered} top = near \cdot \tan \left( {\frac{\pi }{180} \cdot FOV/2} \right) \\ bottom = - top \\ right = top \cdot aspect \\ left = - right \\ \end{gathered}\]The projection matrix, P, multiplies the product view matrix model matrix and, basically projects the world coordinates to the unit cube. For a generic vertex, v, this is the way we apply the view and model transformations:
\[v' = P \cdot V \cdot M \cdot v\]Putting the transformations at work
If you remember, in the first article of the OpenGL 101 series, I’ve mentioned the GLM library. GLM is a small mathematical library that implements the transformations presented in this article, matrix/vector operations and much more.
We’ll start with a slightly modified version of ex_11 from our previous article. You will find the complete source code for this article on Github.
Save the project as ex_14 and add the necessary GLM headers to the code:
1 #include <glm/glm.hpp>
2 #include <glm/gtc/matrix_transform.hpp>
3 #include <glm/gtc/type_ptr.hpp>In the initialize function we start by creating the model, view and projection matrices:
1 glm::mat4 Model, View, Projection;After creation, the above matrices are equal to the identity matrix.
In order to transfer the above three matrices to the vertex shader we’ll add at the end the initialization function:
1 // Transfer the transformation matrices to the shader program
2 GLint model = glGetUniformLocation(shaderProgram, "Model" );
3 glUniformMatrix4fv(model, 1, GL_FALSE, glm::value_ptr(Model));
4
5 GLint view = glGetUniformLocation(shaderProgram, "View" );
6 glUniformMatrix4fv(view, 1, GL_FALSE, glm::value_ptr(View));
7
8 GLint projection = glGetUniformLocation(shaderProgram, "Projection" );
9 glUniformMatrix4fv(projection, 1, GL_FALSE, glm::value_ptr(Projection));And the modified vertex shader program:
1 #version 150
2
3 in vec4 position;
4 in vec2 texture_coord;
5 out vec2 texture_coord_from_vshader;
6
7 uniform mat4 Model;
8 uniform mat4 View;
9 uniform mat4 Projection;
10
11 void main() {
12 gl_Position = Projection * View * Model * position;
13 texture_coord_from_vshader = texture_coord;
14 }Line 12 from the vertex program applies the transformation matrices to every vertex that enter the shader.
If you run the above code, this is what you should see:
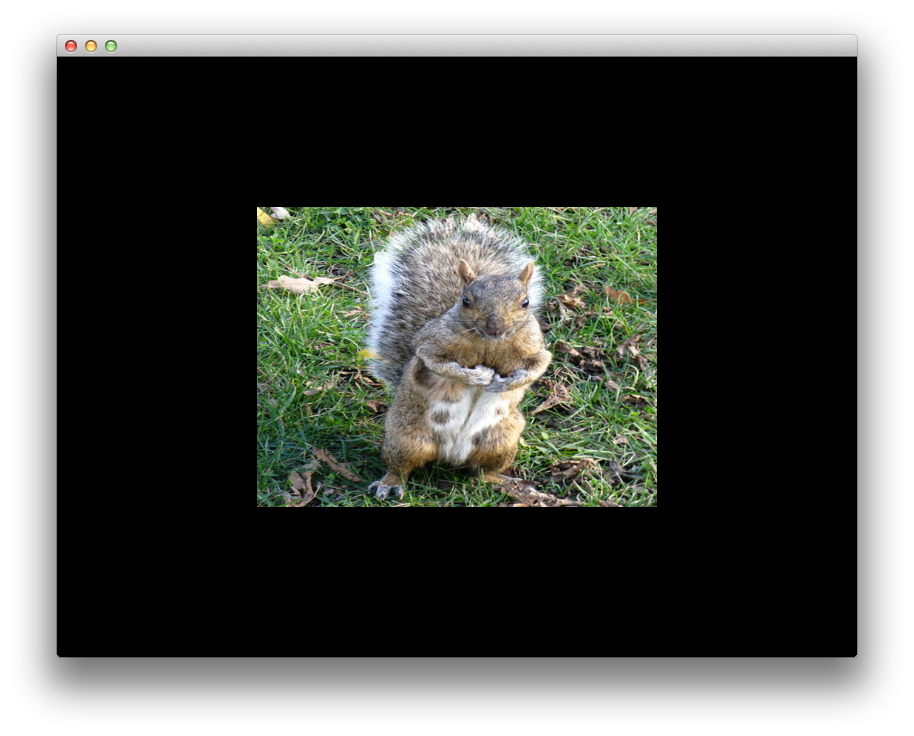
Obviously, the object is not altered by our unitary matrices multiplications. However, the square from the center of the image looks more like a rectangle. This is because the aspect ratio of our window 800:600 will distort the length of any segment that is not parallel with the Oy axis. We can correct this effect in two ways:
-
Using a window with a 1:1 aspect ratio;
-
Using the projection matrix to compensate the distortion of our window.
Let’s try to use the second solution, we start by imposing:
\[\frac{width}{height} = \frac{right - left}{top-bottom}\]We fix the width, height, top, bottom and we have:
\[right - left = \frac{width \cdot (top - bottom)}{height}\]from where:
\[right = \frac{width \cdot (top - bottom)}{2 \cdot height}\]and
\[left = -right\]GLM allow us to create a project matrix with glm::ortho(left, right, bottom, top, near, far), in our particular case we can use:
1 glm::mat4 Model, View, Projection;
2
3 // Set the projection matrix
4 Projection = glm::ortho(-4.0f/3.0f, 4.0f/3.0f, -1.0f, 1.0f, -1.0f, 1.0f);If you run the above code, you should see:
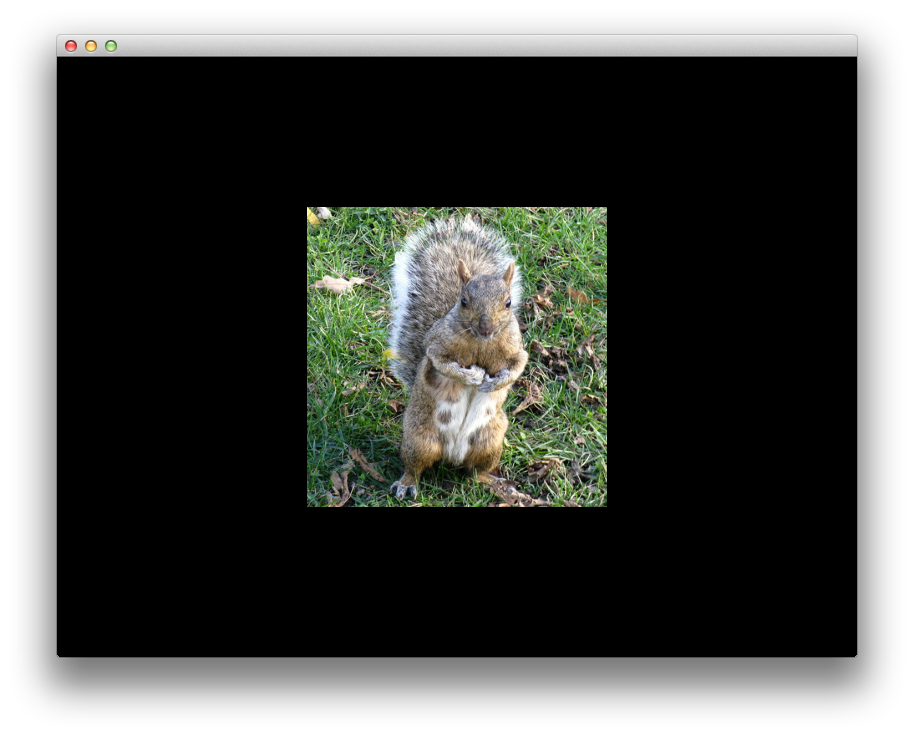
Let’s apply a translation and a 45 degrees rotation to our object.
1 glm::mat4 Model, View, Projection;
2
3 // Set the projection matrix
4 Projection = glm::ortho(-4.0f/3.0f, 4.0f/3.0f, -1.0f, 1.0f, -1.0f, 1.0f);
5
6 // Translation
7 Model = glm::translate(Model, glm::vec3(0.1f, 0.2f, 0.5f));
8
9 // Rotation around Oz with 45 degrees
10 Model = glm::rotate(Model, 45.0f, glm::vec3(0.0f, 0.0f, 1.0f));At line 7 glm::translate expects as parameters: the model matrix, and a vector with where you want the object to be translated \(T_x, T_y, T_z\), corresponding to the translation matrix presented earlier.
glm::rotate expects as parameters: the model matrix, the rotation angle in degrees and the rotation axis.
Please note that GLM expects the angles in degrees, while the default in C++ is to use the angles in radians.
If you run the above code, you should see:
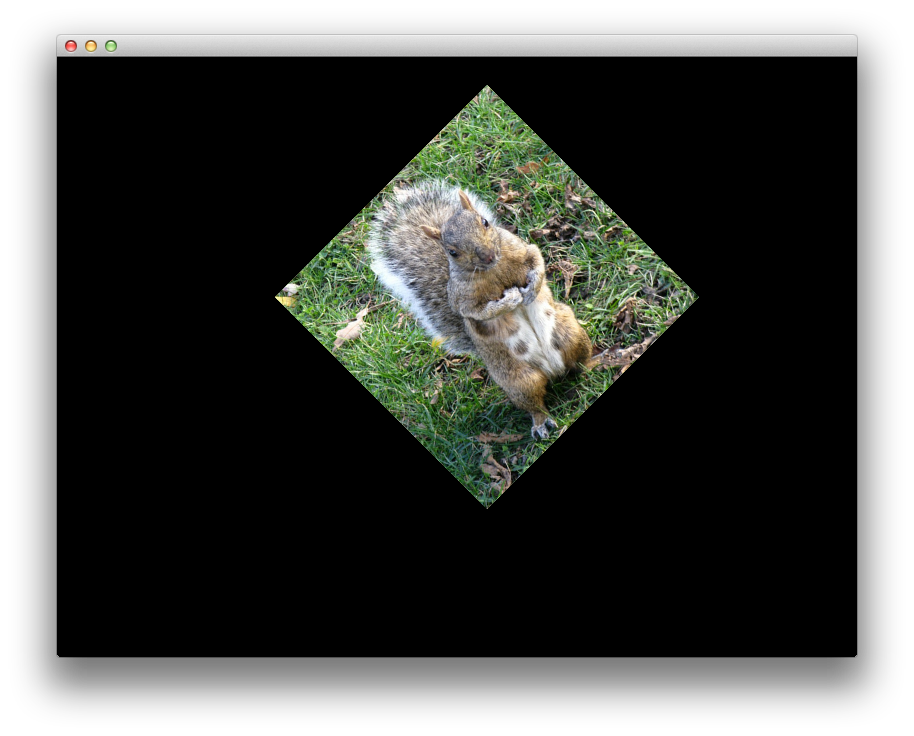
In the next article we are going to start drawing 3D bodies.
All posts from this series:
- OpenGL 101: Windows, OS X and Linux - Getting Started
- OpenGL 101: Drawing primitives - points, lines and triangles
- OpenGL 101: Textures
- OpenGL 101: Matrices - projection, view, model
If you are interested in learning more about Math for computer graphics and game programming, I would recommend reading Mathematics for 3D Game Programming and Computer Graphics by Eric Lengyel:
Another good book about Math in computer graphics and game programming is 3D Math Primer for Graphics and Game Development by F. Dunn and I. Parberry:
A good book about modern OpenGL is OpenGL SuperBible by G. Sellers, S Wright and N. Haemel:


