Sorting data in parallel CPU vs GPU

Posted on February 4, 2013 by Paul

The code for this post is on GitHub: https://github.com/sol-prog/Sort_data_parallel.

You can read the second part of this article.

For many programmers sorting data in parallel means implementing a state of the art algorithm in their preferred programming language. However, most programming languages have a good serial sorting function in their standard library. It appears to me, that the obvious thing to do is to first try to use what your language library provides. If this approach is not successful, you should try to find an existing library that is used, and consequently well debugged, by other programmers. Only as a last resort, you should implement a new sorting algorithm from scratch.

In the case of C++, we have a well tested sorting function in the STL, std::sort, unfortunately std::sort will use only a fraction of the processing power available in a modern multicore system.

Suppose now, that you have two sorted arrays and your task is to combine them as a single sorted array. We are fortunate enough to have a function made just for these kind of situations - std::merge. This means, in a nutshell, that when we need to sort some data, we can split this data in a few pieces, sort each piece of data in a separate thread and use std:merge to combine the sorted pieces - a poor man’s parallel merge-sort algorithm.

In the next figure I’ve tried to exemplify the above idea. We start, for e. g., with a ten elements array. We split this array in four chunks, after this, each chunk of data is passed to std::sort in a separate thread. We end up with four chunks of sorted elements. Now, we can use std::merge to combine the sorted data also in parallel, in pairs, we do this until we end up with a single piece of data. Please note that the numbers in the next diagram represents array indices:

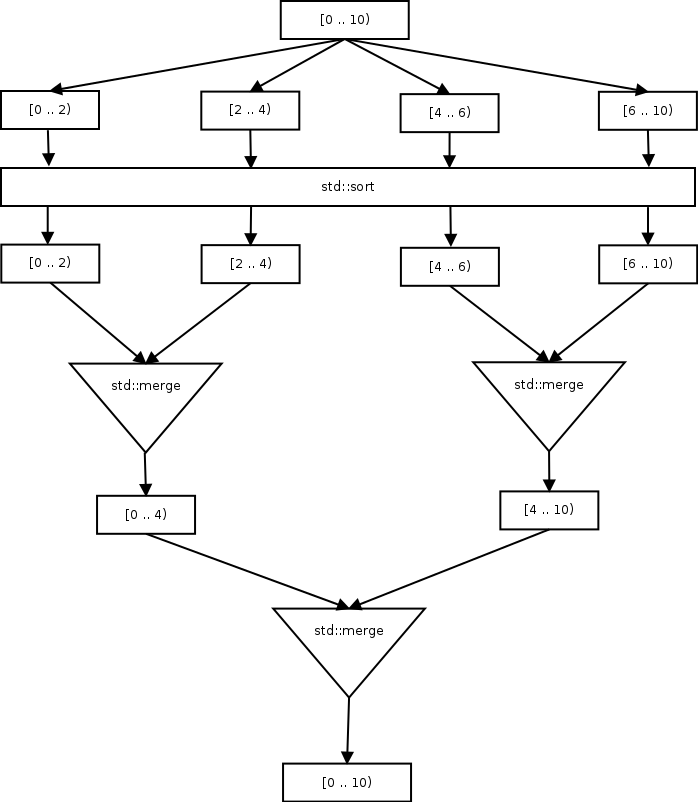
We can take a concrete example to see how the algorithm works:

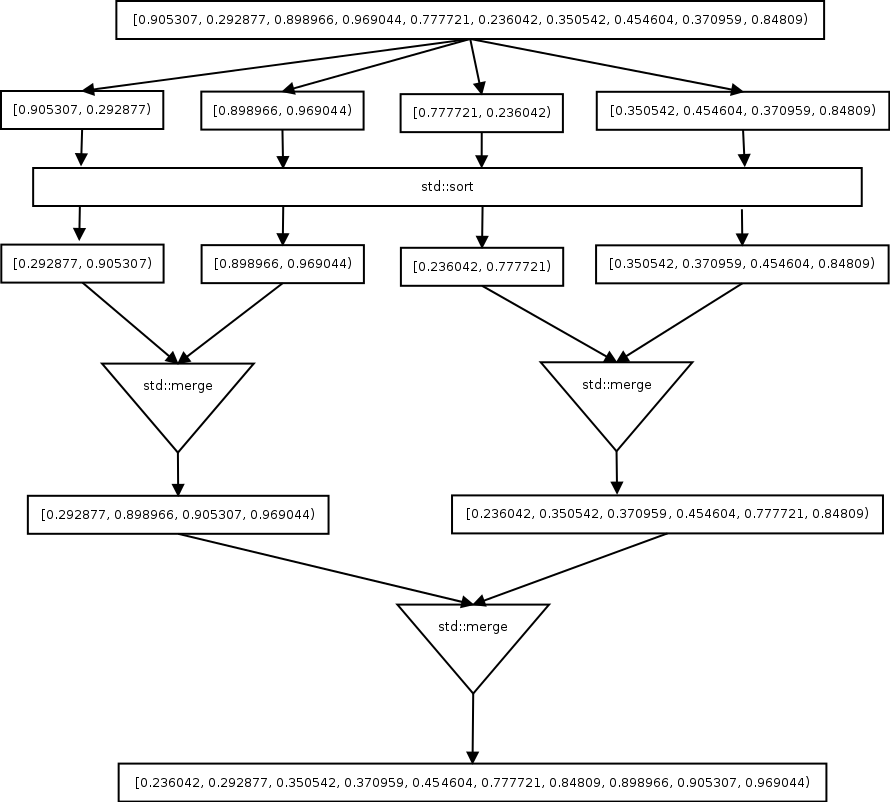
In order to implement the above algorithm in C++, we start by implementing two helper functions, one for partitioning the data and one for filling an array with random numbers:

 1 //Split "mem" into "parts", e.g. if mem = 10 and parts = 4 you will have: 0,2,4,6,10
 2 //if possible the function will split mem into equal chuncks, if not
 3 //the last chunck will be slightly larger
 4 std::vector<size_t> bounds(size_t parts, size_t mem) {
 5     ...
 6 }
 7 
 8 //Fill a vector with random numbers in the range [lower, upper]
 9 void rnd_fill(std::vector<double> &V, const double lower, const double upper, const unsigned int seed) {
10     ...
11 }

You can see the complete code for the above functions on the Github repository for this post.

Next, we list the C++ functions that implements our version of the parallel merge-sort algorithm:

 1 //Use std::sort
 2 void test_sort(std::vector<double> &V, size_t left, size_t right) {
 3     std::sort(std::begin(V) + left, std::begin(V) + right);
 4 }
 5 
 6 //Merge V[n0:n1] with V[n2:n3]. The result is put back to V[n0:n3]
 7 void par_merge(std::vector<double> &V, size_t n0, size_t n1, size_t n2, size_t n3) {
 8     ...
 9 }
10 
11 // Combine std::sort and std::merge to sort data in parallel
12 double run_tests(std::vector<double> &V, size_t parts, size_t mem) {
13 
14     //Split the data in "parts" pieces and sort each piece in a separate thread
15     std::vector<size_t> bnd = bounds(parts, mem);
16     std::vector<std::thread> thr;
17 
18     auto start = boost::chrono::steady_clock::now();
19 
20     //Launch "parts" threads
21     for(size_t i = 0; i < parts; ++i) {
22         thr.push_back(std::thread(test_sort, std::ref(V), bnd[i], bnd[i + 1]));
23     }
24 
25     for(auto &t : thr) {
26         t.join();
27     }
28 
29     //Merge data
30     while(parts >= 2) {
31         std::vector<size_t> limits;
32         std::vector<std::thread> th;
33         for(size_t i = 0; i < parts - 1; i += 2) {
34             th.push_back(std::thread(par_merge, std::ref(V), bnd[i], bnd[i + 1], bnd[i + 1], bnd[i + 2]));
35 
36             size_t naux = limits.size();
37             if(naux > 0) {
38                 if(limits[naux - 1] != bnd[i]) {
39                     limits.push_back(bnd[i]);
40                 }
41                 limits.push_back(bnd[i + 2]);
42             }
43             else {
44                 limits.push_back(bnd[i]);
45                 limits.push_back(bnd[i + 2]);
46             }
47         }
48 
49         for(auto &t : th) {
50             t.join();
51         }
52 
53         parts /= 2;
54         bnd = limits;
55     }
56     auto end = boost::chrono::steady_clock::now();
57 
58     return boost::chrono::duration <double, boost::milli> (end - start).count();
59 }

run_tests will return the time, in milliseconds, in which we can sort in parallel the vector V.

The above code is 100% portable on any modern operating system that has a standard C++11 compiler.

Suppose now, that your machine has a CUDA capable GPU. What will be the easiest way to sort an array of data on the GPU ? With CUDA 5 and Thrust we can sort an array in a few lines of code:

 1     ...
 2 
 3     std::vector<double> V;
 4     thrust::device_vector<double> d_V;
 5 
 6     ...
 7 
 8     //use the system time to create a random seed
 9     unsigned int seed = (unsigned int) time(NULL);
10 
11     rnd_fill(V, 0.0, 1.0, seed);
12     d_V = V; // Transfer V on GPU
13 
14     cudaEvent_t start, stop;
15     cudaEventCreate(&start);
16     cudaEventCreate(&stop);
17 
18     //Start recording
19     cudaEventRecord(start,0);
20 
21     thrust::stable_sort(d_V.begin(), d_V.end());
22 
23     //Stop recording
24     cudaEventRecord(stop,0);
25     cudaEventSynchronize(stop);
26     float elapsedTime;
27     cudaEventElapsedTime(&elapsedTime, start, stop);
28 
29     cudaEventDestroy(start);
30     cudaEventDestroy(stop);
31 
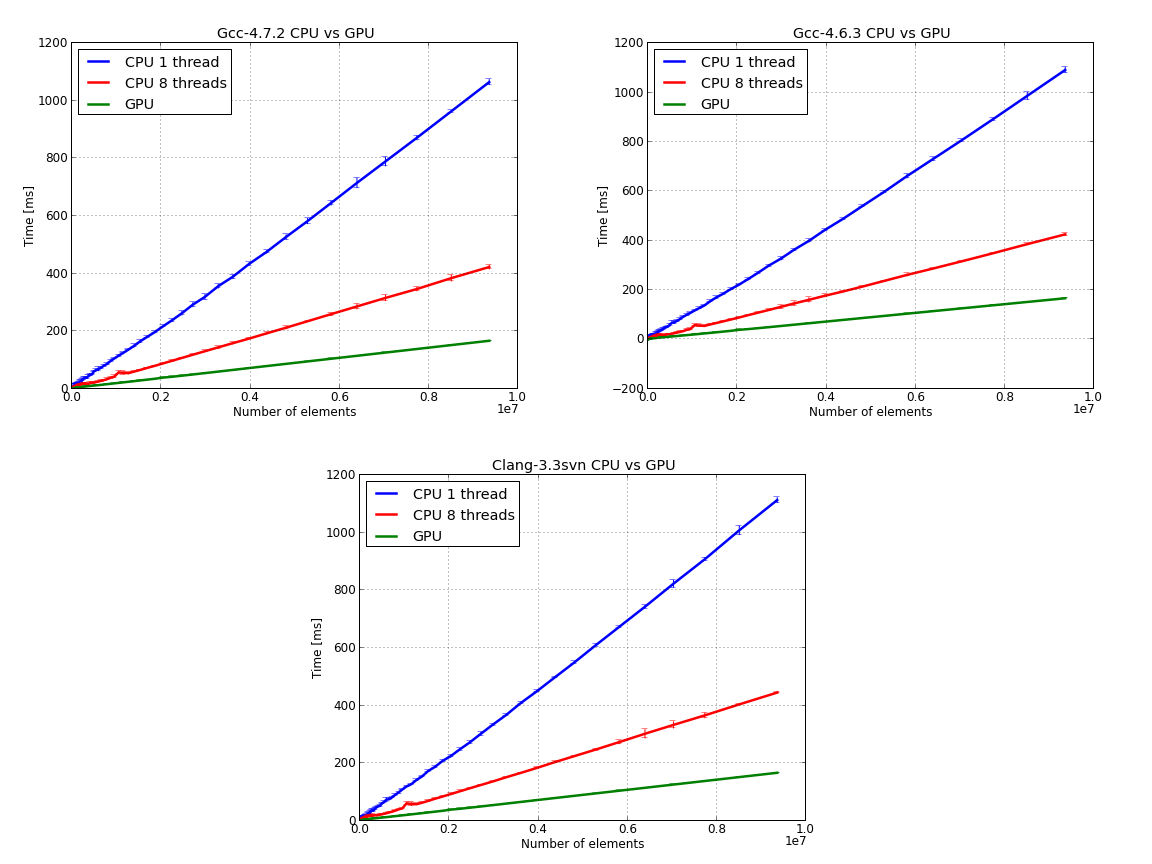
32     ...

I’ve benchmarked the above codes, CPU and GPU, on an Intel i7 Q740, 16 GB RAM, NVIDIA GeForce GT 445M with 3 GB RAM machine that runs Ubuntu 12.04. The test data was a random array of double precision numbers with 10 to 10 millions elements. The CPU code was tested in serial (single thread) and parallel (eight threads) mode.

I’ve used three C++ compilers: gcc-4.6.3 which is the default compiler on Ubuntu 12.04, gcc-4.7.2 and Clang-3.3svn with libc++. If you are interested in building from sources gcc-4.7.2 and Clang-3.3 you can consult this and this. Each test was repeated one hundred times, the data was averaged and we’ve calculated the standard deviation.

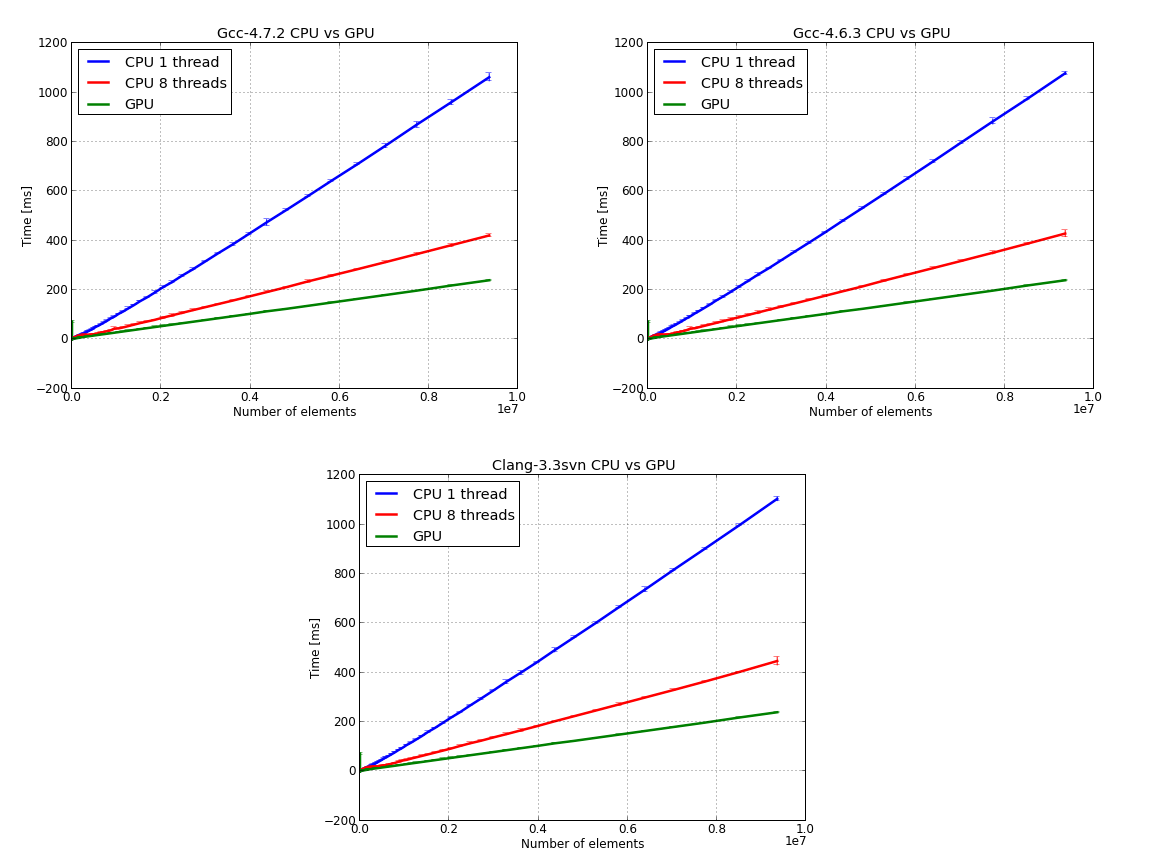
Next image presents the raw data - time versus number of elements for CPU 1/8 threads and for the GPU:

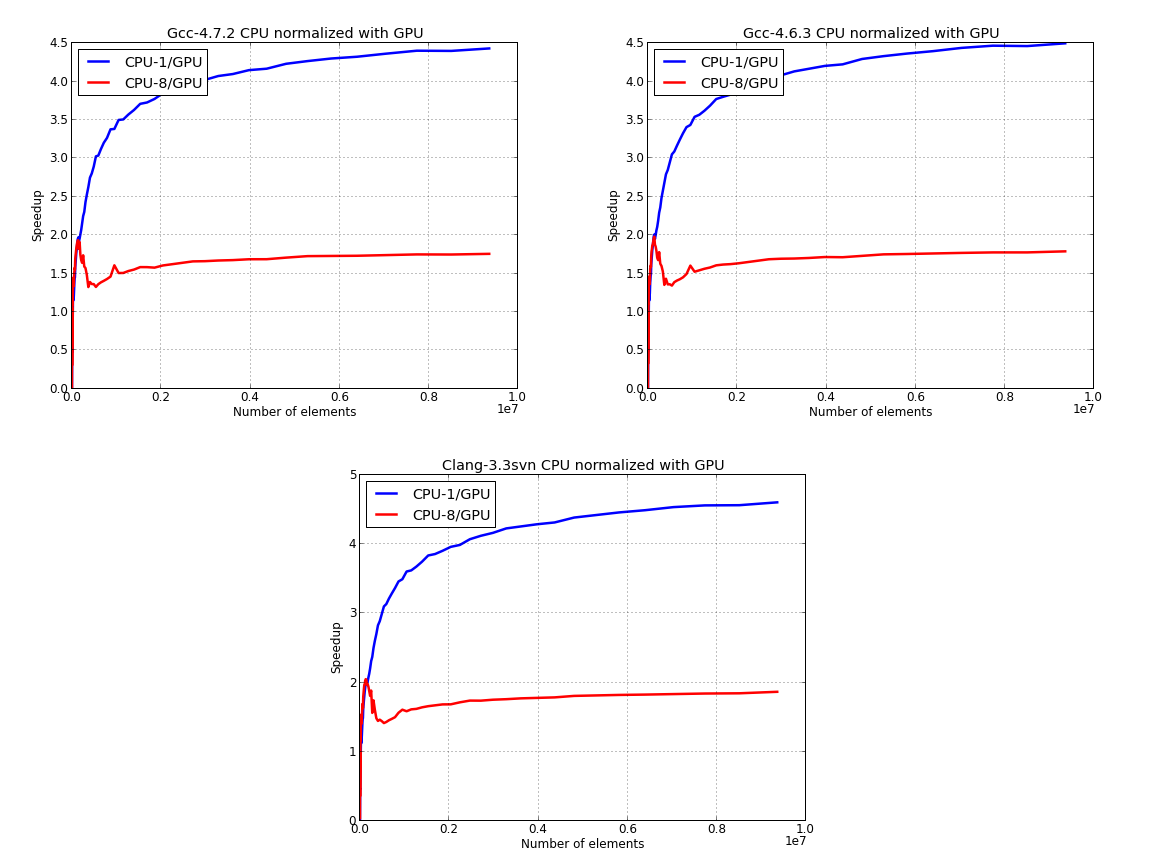
Here, we’ve used the GPU time to normalize the data for the CPU:

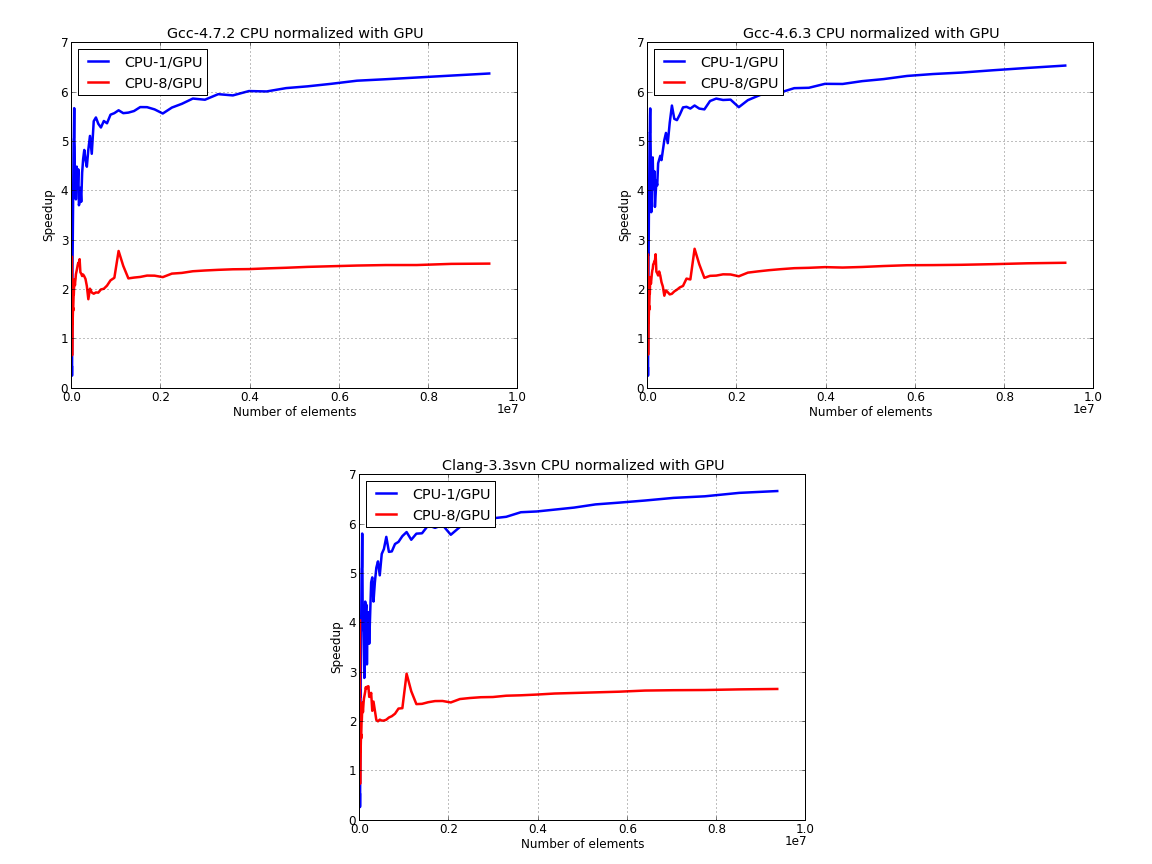
Next figure presents the data for CPU only, where we’ve used the parallel data to normalize the results:

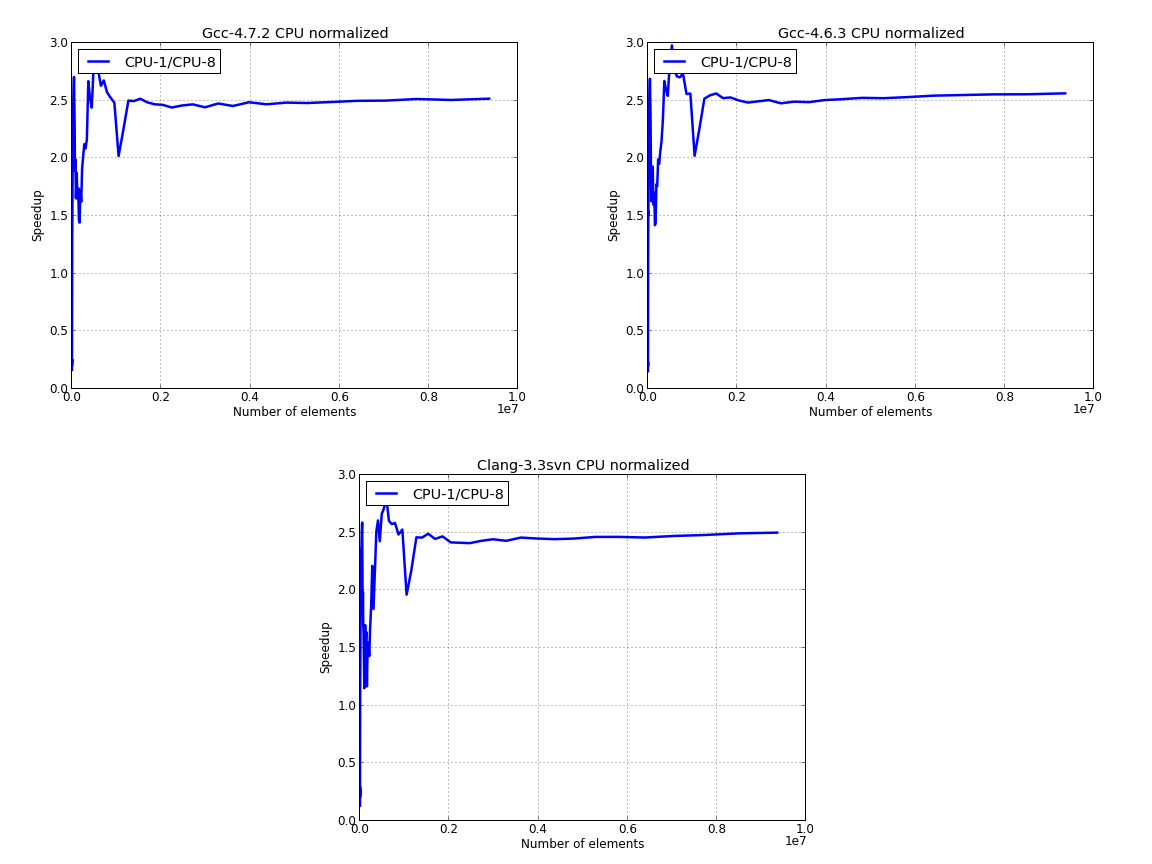
The last image suggests that using the building blocks of the STL we can obtain about 2.5 speedup for sorting data in parallel versus the serial version.

In the next table, we present the size in bytes of the executable generated by each compiler:

I’ve received a few messages about not taking into consideration the cost of moving data from CPU to GPU and the other way around. Your complaints were heard. In the next set of figures the GPU time contains the cost of moving the data back and forth. Also, I’ve replaced the data for the single thread test with a single call to std::sort. The original and the modified code is on Github. Without further ado let’s see the figures.

The raw data - time versus number of elements for CPU 1/8 threads and for the GPU:

Here, we’ve used the GPU time to normalize the data for the CPU:

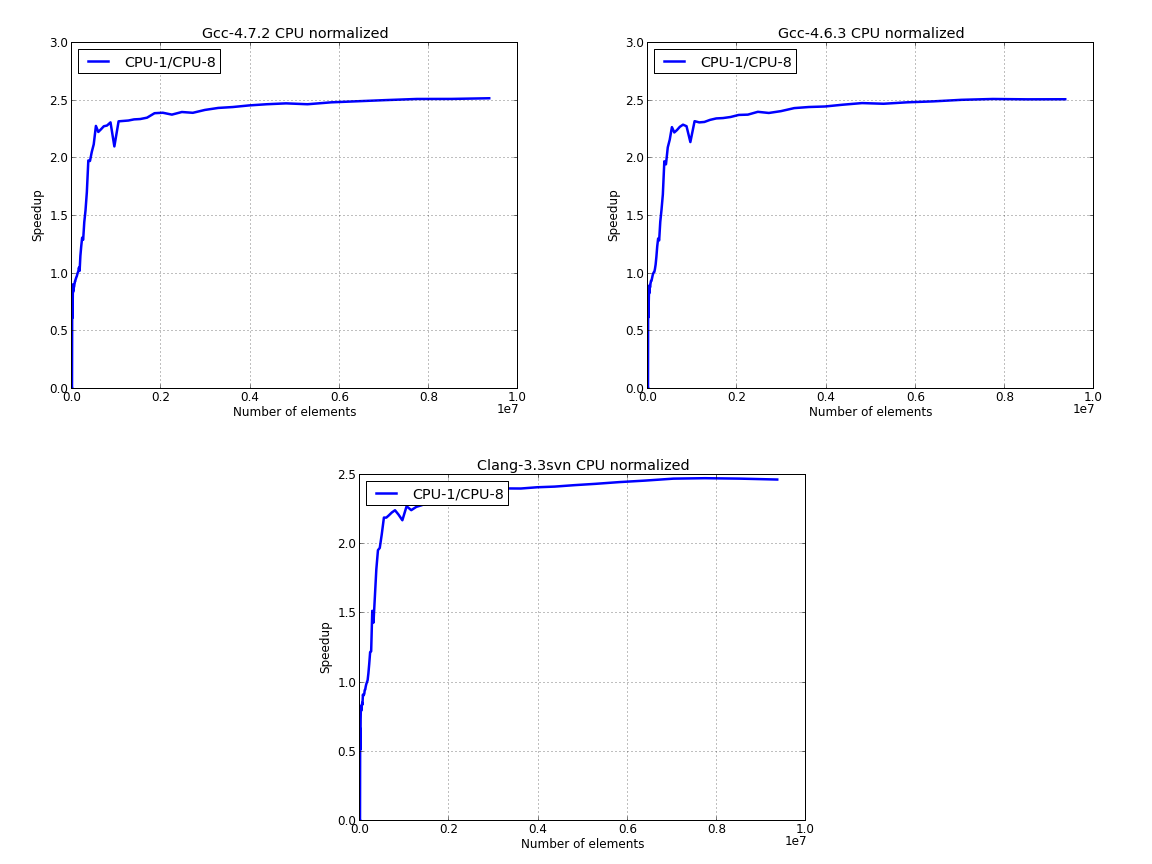
Last image presents the data for CPU only, where we’ve used the parallel data to normalize the results:

If you are interested in learning more about the C++11 Standard Library, I would recommend reading The C++ Standard Library: A Tutorial and Reference (2nd Edition) by N. M. Josuttis:

or Professional C++ by M. Gregoire, N. A. Solter, S. J. Kleper 2nd edition: