C++17 constexpr everything (or as much as the compiler can)

Posted on December 27, 2017 by Paul

During the holidays I did some catch up with CppCon 2017. One of the titles that I had on my to watch list for a few months now was constexpr ALL the Things! by Bean Deane and Jason Turner. Please note that I wrote most of this article before actually watching the presentation.

The title of the presentation made me curious if I can optimize an old piece of code that used a huge 2D array of coefficients as the initial condition for a long calculation. In order to avoid recalculating the big array of coefficients, I used to keep them in a file and simply load the data in memory every time the code was executed. The promise of using a constexpr was that I could avoid keeping two executables (the code that generated the coefficients and the code that did the actual work) and a data file. Replacing everything with a single binary was interesting and could potentially be faster.

In order to test the above, I devised a simpler model - fill an array with data generated at compile time.

Let’s start with a simple example that calculates the factorial of a number recursively (my old code used a recursive relation to generate the coefficients, so this was pretty close to what I needed):

1 #include <iostream>
2 
3 constexpr int factorial(int n) {
4     return n <= 1 ? 1 : (n * factorial(n - 1));
5 }
6 
7 int main() {
8     std::cout << factorial(5) << '\n';
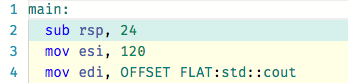
9 }

If you compile the above code with GCC 7.2 or Clang 5, the compiler will replace the call to factorial(5) with 120 at compile time, as expected. You can see the complete assembly code generated by both compilers. Here is a snippet of the assembly code generated by GCC:

A slightly more complicated example is to calculate the Fibonacci numbers using a constexpr function:

 1 #include <iostream>
 2 
 3 constexpr int factorial(int n) {
 4     return n <= 1 ? 1 : (n * factorial(n - 1));
 5 }
 6 
 7 constexpr int fibonacci(unsigned n) {
 8     return n <= 1 ? n : fibonacci(n - 1) + fibonacci(n - 2);
 9 }
10 
11 int main() {
12     std::cout << factorial(5) << '\n';
13     std::cout << fibonacci(10) << '\n';
14 }

GCC 7.2 will replace the call to fibonacci(10) with 55, as expected. Turns out that (for this particular usage) Clang 5 can’t calculate the recursive Fibonacci function at compile time, you can see the complete generated assembly. Here is a snippet of the assembly code generated by Clang:

This is not good! My original code has a more complicated recursive relation than the above Fibonacci implementation.

You can force Clang to behave by saving the value first:

 1 int main() {
 2     constexpr int a = factorial(12);
 3     constexpr int b = fibonacci(10);
 4 
 5     // Check if the values are actually calculated at compile time
 6     static_assert(a == 479001600, "factorial failed\n");
 7     static_assert(b == 55, "fibonacci failed\n");
 8 
 9     std::cout << a << '\n';
10     std::cout << b << '\n';
11 }

You can see the generated assembly for the above code here.

Noe, let’s try with an iterative implementation:

 1 #include <iostream>
 2 
 3 constexpr int fibonacci(int n) {
 4     int F0{0};
 5     int F1{1};
 6     int F{};
 7 
 8     if(n <= 1) {
 9         return n;
10     } else {
11         for(int i = 2; i <= n; ++i) {
12             F = F0 + F1;
13             F0 = F1;
14             F1 = F;
15         }
16         return F;
17     }
18 }
19 
20 int main() {
21     std::cout << fibonacci(10) << '\n';
22 }

For the iterative implementation both compilers generate the value of the function at compile time as expected, you can see the complete generated assembly here. The call to fibonacci(10) is replaced with 55.

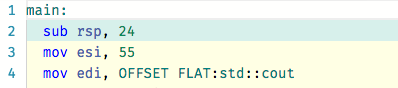
Here is a snippet of the assembly generated by GCC:

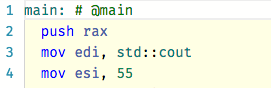
and for Clang:

Next problem, is how do you store a bunch of generated values in an array. If you need a small number of values, a simple approach is to directly initialize the array, e.g.:

 1 #include <array>
 2 #include <iostream>
 3 
 4 constexpr int fibonacci(int n) {
 5     // ... same code as above ...
 6 }
 7 
 8 int main() {
 9     constexpr std::array values{fibonacci(8), fibonacci(9), fibonacci(10)};
10     std::cout << values[1] << '\n';
11     std::cout << values[2] << '\n';
12 }

You can see the complete generated assembly here. The code works as expected with both compilers and the values are calculated at compile time. Please note that the above example also works if you replace std::array with a C type array:

 1 #include <iostream>
 2 
 3 constexpr int fibonacci(int n) {
 4     // ... same code as above ...
 5 }
 6 
 7 int main() {
 8     constexpr int values[]{fibonacci(8), fibonacci(9), fibonacci(10)};
 9     std::cout << values[1] << '\n';
10     std::cout << values[2] << '\n';
11 }

What about the case when you need to generate a large number of elements? A simple approach is to generate these values with a separate constexpr function that returns the filled array, example:

 1 #include <array>
 2 #include <iostream>
 3 #include <cstdint>
 4 
 5 constexpr uint64_t fibonacci(uint64_t n) {
 6     uint64_t F0{0};
 7     uint64_t F1{1};
 8     uint64_t F{};
 9 
10     if(n <= 1) {
11         return n;
12     } else {
13         for(uint64_t i = 2; i <= n; ++i) {
14             F = F0 + F1;
15             F0 = F1;
16             F1 = F;
17         }
18         return F;
19     }
20 }
21 
22 const uint64_t NN = 50;
23 constexpr std::array<uint64_t, NN> fill_array() {
24     std::array<uint64_t, NN> v{0};
25     for(uint64_t i = 0; i < NN; ++i) {
26         v[i] = fibonacci(i);
27     }
28     return v;
29 }
30 
31 int main() {
32     constexpr std::array<uint64_t, NN> v = fill_array();
33     std::cout << v[9] << '\n';
34     std::cout << v[10] << '\n';
35 }

You can see the complete generated assembly here. The code works as expected with both compilers and the values are calculated at compile time. (Please note that for large Fibonacci numbers you could easily overflow).

In conclusion, at the time of this writing, you need to inspect the generated code of your compiler, if you want to be sure that something is really calculated at compile time. Alternatively, you can use static_assert to test if a particular value is calculated at compile time. Example:

 1 #include <array>
 2 #include <iostream>
 3 #include <cstdint>
 4 
 5 constexpr uint64_t fibonacci(uint64_t n) {
 6     // ... same code as above ...
 7 }
 8 
 9 const uint64_t NN = 50;
10 constexpr std::array<uint64_t, NN> fill_array() {
11     // ... same code as above ...
12 }
13 
14 int main() {
15     constexpr std::array<uint64_t, NN> v = fill_array();
16 
17     // Compile time tests:
18     static_assert(v[1] == 1, "Test failed! Fibonnaci(1) != 1!\n");
19     static_assert(v[10] == 55, "Test failed! Fibonnaci(10) != 55!\n");
20 }

If you are interested to learn more about modern C++ I would recommend reading A Tour of C++ by Bjarne Stroustrup.

or Effective Modern C++ by Scott Meyers.